![]()
Introduction
Sea-Bird Electronics manufactures instruments for oceanographic research, specializing in temperature, pressure and salinity measurement. We have a keen interest in measurement. As such, we not only work to improve instrument design but to understand the limitations of field measurement and to refine the use of instruments and methods of measurement.
The magnitude of temperature errors in the presence of flow became
evident in measurements of ocean salinity. Salinity is computed from temperature,
conductivity, and pressure measurements that must be coordinated on the same parcel of
water. To accomplish this the water is drawn past temperature and conductivity sensors in
a duct where the flow is carefully controlled by a pump. In Figure 1
below, the temperature difference between two independently pumped temperature sensors
changes when the flow is slowed past the first sensor (A), then restored (B), then flow is
slowed past the second sensor (C), and then restored (D).
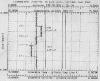
The temperature measurements in this flow stream register too warm due to viscous heating of the probe tip. The error is of order 0.001
°C at 1 m/s and increases as the square root of Prandtl number and velocity squared. It varies mildly with the angle of attack (<15%) and probe shape (<5%). Based on Prandtl number scaling, the error should be greatest in laminar flows and decrease with embedded turbulence by up to a factor of 3 in 0°C water.In turbine efficiency measurements as well as oceanography where mK precision is required, measurement methods must be developed to allow the flow-induced viscous heating errors to be characterized and removed from data. Toward this goal, Sea-Bird has been investigating viscous heating effects with computational fluid dynamics (CFD) models and direct laboratory measurements.
Computational Fluid Dynamics Results
A CFD model of the flow past a temperature probe tip allowed a numerical investigation of the viscous heating phenomenon. It has helped isolate the relevant physics and determine the mathematical dependence of viscous heating on various parameters.
This CFD model implemented the full non-linear Navier-Stokes equation. To reduce the computational complexity only a 2-dimensional computational grid was implemented with corrections for the cylindrical symmetry of the flow. Without a 3-dimensional grid required for turbulence modeling, the flow was constrained to remain laminar. This probably does not reduce the applicability of the model to Sea-Bird sensors used in smooth flows < 10 m/s because the Reynolds numbers do not exceed 20,000 remaining laminar. The extension of these results to turbulent flows is discussed briefly. In all cases a computational run was continued until a steady state flow and temperature condition was reached.
Two flow patterns across the sensors were investigated; axisymmetric flow, with the free stream running parallel to the temperature probe axis, and perpendicular flow, with the free stream running 90 degrees to the probe axis. Within each flow pattern a few different approximations for thermal boundary conditions were investigated.
AXISYMMETRIC FLOW
Model conditions:
• probe geometry is a cylinder with hemispherical tip
• 100 x 100 computational grid on a half-plane through the probe diameter
• log grid spacing from the stagnation point, sub-viscous scale to 11 probe diameters
• equations adjusted for cylindrical nature of flow so that a 3-D grid was not necessary
Adiabatic wall approximation
The CFD program used could not model heat flow inside a solid boundary so a first boundary approximation is an adiabatic sensor probe wall. Heat is allowed to redistribute within the flow by diffusion and advection but no heat is allowed to pass into the probe sheath. The results may be valid if at steady state temperature the net heat flux through the probe surface is small (small stem losses down the probe). Regardless, this approximation gives us the water skin temperature 'forcing function' that acts to heat the sensor probe tip.
More than half of the computational grid is within 1/2 diameter of the probe surface (Figure 2).

Figure 2
A typical steady state flow pattern (Figure 3) has the expected features; stagnation point, viscous boundary layer structure, and flow acceleration and enhanced shear at probe tip (the triangle symbols on this and following figures mark the distance scale with sensor diameter equivalents).
Figure 3
Velocity contour plots (Figure 4) highlight the boundary layer development, and a compressed boundary layer and high shear at the probe tip, and color-flooded velocity contours (Figure 5) visually enhance the flow patterns.
Figure 4
Figure 5
The temperature distribution (Figure 6) that results from viscous heating in the flow shear has three notable features; no heating at the stagnation point, a peak in heating under the region of accelerated flow, and a near constant skin temperature under the down-stream boundary layer.
Figure 6
The skin temperature of water along the probe surface rises through a peak and settles to a constant value (Figure 7).
Figure 7
The 'over'-temperature experienced by the thermistor bead inside the metal probe sheath is an average of the skin temperature from the probe tip back perhaps 1 to 3 bead diameters (sheath diameters). This area-weighted average temperature is the second curve (Figure 7). At two diameters back from the probe tip the average temperature is within 0.1 mK (5%) of the temperature averaged for 10 diameters back (dashed asymptote).
Using the average probe tip temperature from computational runs at several velocities, temperatures, and pressure (Figure 8), the over-temperature is found to vary exactly as (Figure 9)
» 0.339 * (n)^0.5 * (U)^2CFD over-temperature = 1.263e-4 * (Pr)^0.5 * (U)^2
n = kinematic viscositywhere :
U = free stream velocity
Pr = Prandtl number = (n r Cp / k)
It is apparent that the downstream boundary layer keeps the probe surface temperature remarkably constant. The assumption of small stem-conduction losses of heat down the probe metal sheath would seem to be reasonable. There is very little surface temperature forcing to drive heat down the sheath and local viscous heating at distances down the probe length balance any stem losses.
Sensor tip geometry
The over-temperature of the probe tip is not very sensitive to tip geometry. Two alternate tip shapes were modeled (Figure 10); a blunted nose (A), and a more stream-lined elliptical tip geometry (B). While the specific temperature distribution at the probe tip is different within the first diameter, the area-weighted average temperatures from all probe shapes agree to better than 5% when averaged 1 or more diameters back from the tip (Figure 11).
Figure 10
Figure 11
Isothermal wall approximation
To investigate the effect of heat redistribution by the sensor metal sheath, the next computational approximation was to consider heat flux through the sheath wall. We assume that the net flux of heat through the probe surface is zero, and that the metal sheath reaches a constant temperature. This is likely satisfied by the higher thermal conductivity of metal (
n=14.6) than water (n=0.59) and low stem-conduction losses due to the probe length (50 diameters length and small metal cross-sectional area). Computational runs, at constant flow conditions, are iterated until a probe surface temperature is found which results in a zero net heat flux through the probe surface (forward 11 diameters of the model).The heat flux distribution for two probe temperatures shows the anticipated form (Figure 12); a large heat flux into the probe surface under the region of accelerated flow at the tip and out of the probe at the stagnation point and downstream in the boundary layer. Only a few iterations are required to find a probe temperature that results in zero integrated (net) heat flux through the probe surface (Figure 13).
Figure 12
Figure 13
The final probe temperatures for this 'isothermal wall' approximation are nearly identical to the adiabatic wall approximation (inset table, Figure 14). The isothermal wall temperatures are less than 1% warmer and have the same dependence on flow speed and Prandtl number.
Figure 14
Angle of attack approximation
A full 3-dimensional flow model would be required to investigate the angle of attack dependence of probe tip temperatures. We chose a starting approximation that preserved a 2-dimensional computational grid, and made CFD calculations of flow perpendicular to the axis of an infinitely long cylinder. This geometry is reasonably applicable to sensors with the probe tip oriented 90 degrees to the flow vector and probably under-estimates temperatures at a real probe tip of finite length.
PERPENDICULAR FLOW
Model conditions:
• probe geometry is an infinitely long cylinder
• 100 x 17 computational grid on a half-plane perpendicular to the probe axis
• log grid spacing from the stagnation point, sub-viscous scale to 10 probe diameters
• flow is also constrained to be steady; no vortex sheet shedding
Adiabatic wall approximation
Following the approximations used in the axisymmetric flow runs the first computational approximation is an adiabatic probe wall. We would expect less tip temperature deviation from stem-loss in a real probe in this orientation because of the efficient local heating source along the entire length of the probe. Again, this approximation does define the water skin temperature 'forcing function' to the probe sheath.
The resulting flow pattern across the cylinder has the anticipated features (Figure 15); a stagnation point, viscous boundary layer structure with flow acceleration and enhanced shear, and a slow recirculation region in the wake of the cylinder.
Figure 15
The color-flooded flow contours highlights the speed and shear patterns (Figure 16).
Figure 16
The resulting temperature distribution in the water exhibits very localized heating only under the region of accelerated flow over the cylinder rim (Figure 17).
Figure 17
The skin temperature along probe surface rises through a peak at the cylinder rim and retains a constant low value in the wake region due to heated boundary layer water entrained into the recirculating flow (Figure 18).
Figure 18
The 'over'-temperature experienced by a thermistor bead inside the metal probe sheath is an average of the surface temperature around the cylinder. The area-weighted average temperature is the second curve (Figure 18) and yields about 1.2 mK above ambient at 2 m/s in contrast to 1.9 mK in the axisymmetric case. The adiabatic wall may not be a good approximation for this flow orientation because heat is likely to redistribute quickly and efficiently along the short circumferential path in the probe metal sheath.
The over-temperature has the same functional dependence on flow speed and viscosity as in the axisymmetric geometry but with a smaller scaling coefficient for the adiabatic wall case.
» 0.214 * (n)^0.5 * (U)^2CFD over-temperature = 0.797e-4 * (Pr)^0.5 * (U)^2
Isothermal wall approximation
In the perpendicular flow case the isothermal wall approximation is more applicable because of the short circumferential distances that heat can be easily transferred in the metal sheath wall. The same approach is taken where computational runs, at constant flow conditions, are iterated until a probe surface temperature is found which results in a zero net heat flux through the circumferential probe surface.
As in the axisymmetric case the heat flux distribution for three probe temperatures shows the anticipated form (Figure 19); a large heat flux into the probe surface under the region of accelerated flow at the upstream edge of the cylinder rim and out of the probe at the stagnation point and in the downstream wake.
Figure 19
However, the average wall temperatures increase 30% above the adiabatic wall approximation to 1.56 mK, because the wall in the wake region of the flow can be heated fairly effectively by spot heating at the upstream cylinder rim (Figure 20).
Figure 20
Extension of the Results to Turbulent flows
To date the CFD models have not been extended to full 3-dimensional flow, a requirement for meaningful computations of turbulent flows. However, the scaling of the viscous heating results with Prandtl number do predict a decrease in the wall temperature as turbulence develops within a constant mean flow and the Prandtl number decreases toward 1. The scaling for laminar flow on a flat plate goes as (Pr)^1/2, whereas for high speed turbulent air flows it goes as (Pr)^1/3 (Schlichting, 1979).
The Prandtl number of ocean water at 2
°C is 12.4. The available scaling suggests a decrease in the wall temperature of a factor of 3.5 to 2.3 if turbulence embedded within a flow of this water drove the Prandtl number to 1.Further investigation of the viscous heating effect in turbulent flows is probably necessary for a full understanding of the turbine efficiency monitoring application.
Laboratory Measurements of viscous heating
The CFD models presented above were run to verify laboratory investigations of the viscous heating effects to Sea-Bird sensors under oceanographic conditions. The agreement between lab measurements and CFD results is very close and lends credence to the applicability of the CFD findings to the field measurements.
Laboratory measurements of temperature (and temperature difference) were made with the 'TC-ducted' configuration of Sea-Bird sensors used in the oceanographic application. (A schematic of the flow path is shown in Figure 21).
Figure 21
Using two pairs of ducted sensors the temperature of a stable bath could be measured by two temperature sensors and the temperature difference measured as the flow in one duct was reduced in successive increments toward zero (Figure 22).
Figure 22
These temperature difference data are then plotted against the reduced flow value and an immediate dependence on velocity and ambient temperature (fluid viscosity) is evident (Figure 23); the symbols are measurements and the curves are U^2 fits to the data.
Figure 23
Renormalizing the temperature difference data to be zero difference at zero flow (Figure 24) demonstrates the agreement of functional form and magnitude with the CFD results (Figure 9).
Figure 24
Tests of 12 different sensors yield the same functional dependencies but apparent differences in magnitude of ±20% (Figure 25). Sensors of different sheath diameters are included in this group. We now suspect that part of this variability derives from a combination of variation in sensor tip shape, diameter and flow accelerations in the test apparatus.
Figure 25
Summary
Temperature measurements in flowing water are affected at the mK level by viscous heating of the sensor tip. In the laminar regime both CFD models and laboratory measurements exhibit a temperature rise of about 1.3e-4 Pr^0.5 U^2. Laboratory measurements indicate that this scaling is applicable, within ± 20%, to a wide range of sensors. Sensitivity to sensor tip geometry is well within ± 5%, to probe diameter (less than 0.5 cm) is within ± 10%, and to angle of attack is probably well within ± 10%.
While no work has been done here in turbulent flows, the Prandtl number scaling of viscous heating predicts a reduction in magnitude by a factor of 2 to 3 in fully developed turbulence (about 0.7e-4 Pr^0.5 U^2). Where measurement precision of 1 mK and better is required the viscous heating effect must clearly be accounted for. Sea-Bird is interested in accomplishing this goal with the turbine efficiency monitoring community.
Acknowledgments
The CFD work presented here was done by Scott Imlay at AMTEC Engineering, a Seattle area firm. Craig Bishop tirelessly performed the laboratory tests. The primary author claims responsibility for errors and misinterpretations.
References
Schlichting, 1973: Boundary-Layer Theory. McGraw-Hill, New York, 817pp. ISBN 0-07-055334-3
Last modified: 06 April 2007